This week we focuses on the data integrity, Message Authentication Codes.
Define: MAC I=(S, V) defined over (K, M, T):
S(k, m) outputs t in T
V(k, m, t) output ‘yes’ or ‘no’
S stands for signing, V stands for verification.
Secure MACs
Attacker can give Alice m 1 , . . . m q m_1, ... m_q m 1 , ... m q t i ← S ( k , m i ) t_i \leftarrow S(k, m_i) t i ← S ( k , m i ) new valid message/tag pairs (m, t), aka existential forgery , such that:
( m , t ) ∉ { ( m 1 , t 1 ) , . . . , ( m q , t q ) } (m, t) \notin \{(m_1, t_1), ..., (m_q, t_q)\} ( m , t ) ∈ / {( m 1 , t 1 ) , ... , ( m q , t q )} The MAC is secure if attacker cannot generate new (m, t), even for existing message, m i m_i m i A d v M A C [ A , I ] = P r [ C h a l . o u t p u t s 1 ] Adv_{MAC}[A, I] = Pr[Chal. outputs 1] A d v M A C [ A , I ] = P r [ C ha l . o u tp u t s 1 ]
Secure PRF -> Secure MAC
The error bound of PRF is A d v M A C [ A , I F ] ≤ A d v P R F [ B , F ] + 1 / ∣ Y ∣ Adv_{MAC}[A, I_F] \leq Adv_{PRF}[B, F] + 1/|Y| A d v M A C [ A , I F ] ≤ A d v PRF [ B , F ] + 1/∣ Y ∣ I F I_F I F ∣ Y ∣ |Y| ∣ Y ∣
Extend AES(16 bytes) from Small-MAC to Big-MAC:
CBC-MAC , ANSI X9.9, FIPS 186-3HMAC , SSL, IPSec, SSH.
CBC-MAC and NMAC
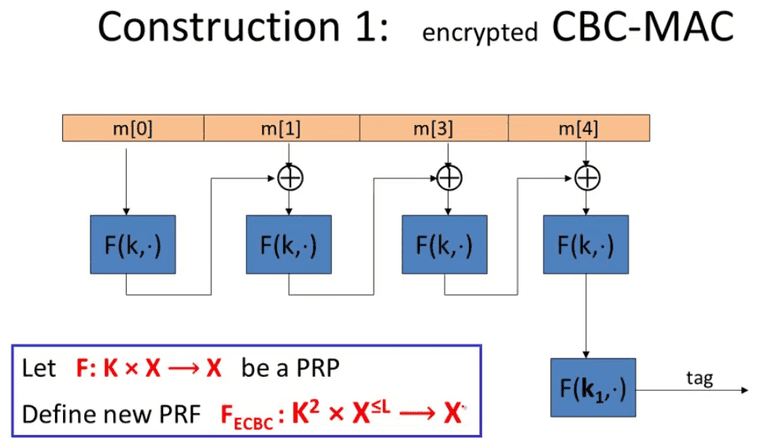
CBC MAC
It is important to use independent k 1 k_1 k 1 raw CBC output.
For raw CBC, the attacker can
choose one block message m, to get t = F(k, m)
then for 2-block message ( m , t ⊕ m ) (m, t\oplus m) ( m , t ⊕ m )
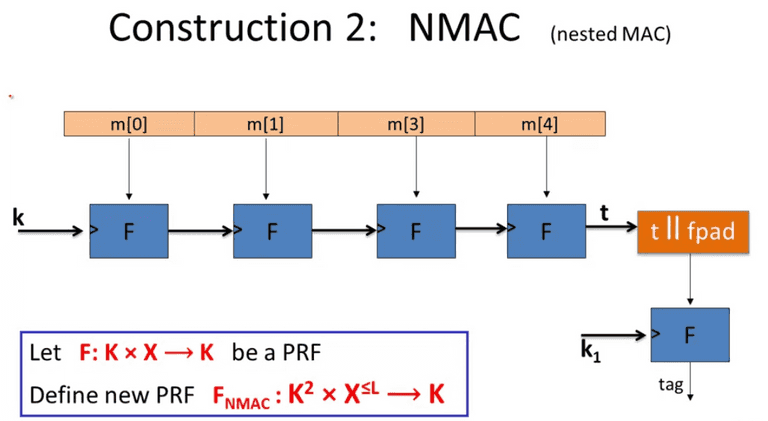
NMAC
Also the independent k 1 k_1 k 1 cascade MAC to make it secure.
A d v P R F [ A , F E C B C ] ≤ A d v P R F [ B , F ] + 2 q 2 ∣ X ∣ A d v P R F [ A , F N M A C ] ≤ q ⋅ L ⋅ A d v P R F [ B , F ] + q 2 2 ∣ K ∣ \begin{align*}
Adv_{PRF}[A, F_{ECBC}] & \leq Adv_{PRF}[B, F] + \frac{2q^2}{|X|} \\
Adv_{PRF}[A, F_{NMAC}] & \leq q \cdot L \cdot Adv_{PRF}[B, F] + \frac{q^2}{2|K|}
\end{align*} A d v PRF [ A , F ECBC ] A d v PRF [ A , F NM A C ] ≤ A d v PRF [ B , F ] + ∣ X ∣ 2 q 2 ≤ q ⋅ L ⋅ A d v PRF [ B , F ] + 2∣ K ∣ q 2 We need to rotate keys for after ∣ X ∣ 1 / 2 |X|^{1/2} ∣ X ∣ 1/2 ∣ K ∣ 1 / 2 |K|^{1/2} ∣ K ∣ 1/2
Once we find a hash collision, we can extend any arbitrary block to mount forgery attack.
MAC padding
Padding MUST be invertible to prevent forgery.
ISO: padding with 10000, 1 indicates the beginning of the padding. In case message has a clear cut, just append a dummy block.
CMAC uses k 1 k_1 k 1 k 2 k_2 k 2
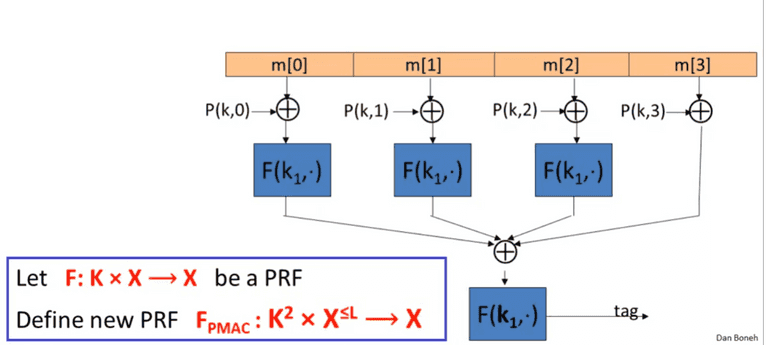
PMAC
Parallel MAC
PMAC
The P ( k , i ) P(k, i) P ( k , i ) k × i k \times i k × i
A d v P R F [ A , F P M A C ] ≤ A d v P R F [ B , F ] + 2 q 2 L 2 ∣ X ∣ Adv_{PRF}[A, F_{PMAC}] \leq Adv_{PRF}[B, F] + \frac{2q^2L^2}{|X|} A d v PRF [ A , F PM A C ] ≤ A d v PRF [ B , F ] + ∣ X ∣ 2 q 2 L 2 It is easy to replace one specific block, and compute the MAC without recomputing everything.
One-time MAC
Kind of like OTP, pick key, ( k , a ) ∈ { 1 , . . . q } 2 (k, a) \in \{1, ... q\} ^2 ( k , a ) ∈ { 1 , ... q } 2 q = 2 128 + 51 q = 2^{128} + 51 q = 2 128 + 51 ( m [ 1 ] , . . . , m [ L ] ) (m[1], ..., m[L]) ( m [ 1 ] , ... , m [ L ])
S ( k e y , m s g ) = ( P m s g ( k ) + a ) m o d q S(key, msg) = (P_{msg}(k) + a)\mod q S ( k ey , m s g ) = ( P m s g ( k ) + a ) mod q where P m s g ( x ) = m [ L ] ⋅ x L + . . . + m [ 1 ] ⋅ x P_{msg}(x) = m[L]\cdot x^L + ... + m[1]\cdot x P m s g ( x ) = m [ L ] ⋅ x L + ... + m [ 1 ] ⋅ x
Many-time MAC
Cater-Wegman MAC:
C W ( ( k 1 , k 2 ) , m ) = ( r , F ( k 1 , r ) ⊕ S ( k 2 , m ) ) CW((k_1, k_2), m) = (r, F(k_1, r)\oplus S(k_2, m)) C W (( k 1 , k 2 ) , m ) = ( r , F ( k 1 , r ) ⊕ S ( k 2 , m )) for F be a secure PRF, for r is random chosen: r ← { 0 , 1 } n r \leftarrow \{0, 1\}^n r ← { 0 , 1 } n V ( k 2 , m , F ( k 1 , r ) ⊕ t ) ) V(k_2, m, F(k_1, r) \oplus t)) V ( k 2 , m , F ( k 1 , r ) ⊕ t ))
Collision Resistance
A function H is collision resistant if for efficient algorithms, the chance to fine the same hash is negligible.
Let I=(S, V) be a MAC for short message over (K, M, T),
Let H: M b i g → M M^{big} \to M M bi g → M
Def: I b i g = ( S b i g , V b i g ) I^{big} = (S^{big}, V^{big}) I bi g = ( S bi g , V bi g ) ( K , M b i g , T ) (K, M^{big}, T) ( K , M bi g , T )
S b i g ( k , m ) = S ( k , H ( m ) ) ; V b i g ( k , m , t ) = V ( k , H ( m ) , t ) S^{big}(k, m) = S(k, H(m)); V^{big}(k, m, t) = V(k, H(m), t) S bi g ( k , m ) = S ( k , H ( m )) ; V bi g ( k , m , t ) = V ( k , H ( m ) , t ) Thm: If I is a secure MAC and H is collision resistant, then I b i g I^{big} I bi g
Birthday Attack
Let H : M → { 0 , 1 } n H:M \to \{0, 1\}^n H : M → { 0 , 1 } n ∣ M ∣ ≫ 2 n |M| \gg 2^n ∣ M ∣ ≫ 2 n O ( 2 n / 2 ) O(2^{n/2}) O ( 2 n /2 )
Let r 1 , . . . , r n ∈ { 1 , . . , B } r_1, ..., r_n \in \{1, .., B\} r 1 , ... , r n ∈ { 1 , .. , B } n = 1.2 × B 1 / 2 n = 1.2 \times B^{1/2} n = 1.2 × B 1/2 P r [ ∃ i ≠ j : r i = r j ] ≥ 1 2 Pr[\exists i \neq j: r_i = r_j] \ge \frac{1}{2} P r [ ∃ i = j : r i = r j ] ≥ 2 1
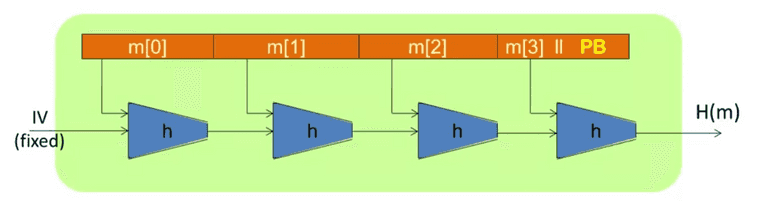
Merkle-Damgard Paradigm
Merkle-Damgard Paradigm
Given h : T × X → T h: T \times X \to T h : T × X → T H : X ≤ L → T H: X^{\le L} \to T H : X ≤ L → T
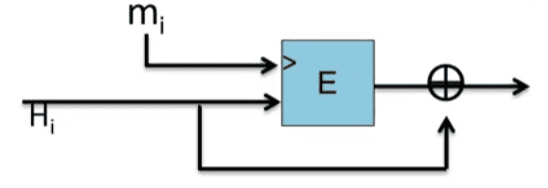
Davies-Meyer compression
E : K × { 0 , 1 } n → { 0 , 1 } n E: K \times \{0, 1\}^n \to \{0, 1\}^n E : K × { 0 , 1 } n → { 0 , 1 } n h ( H , m ) = E ( m , H ) ⊕ H h(H, m)= E(m, H) \oplus H h ( H , m ) = E ( m , H ) ⊕ H
Davies-Meyer compression
Suppose E is an ideal cipher, finding a collision of h ( H , m ) = h ( H ′ , m ′ ) h(H, m) = h(H', m') h ( H , m ) = h ( H ′ , m ′ ) O ( 2 n / 2 ) O(2^{n/2}) O ( 2 n /2 )
Miyaguchi-Preneel:
h ( H , m ) = E ( m , H ) ⊕ H ⊕ m h ( H , m ) = E ( H ⊕ m , m ) ⊕ m \begin{align*}
h(H, m) & = E(m, H) \oplus H \oplus m \\
h(H, m) & = E(H \oplus m, m) \oplus m
\end{align*} h ( H , m ) h ( H , m ) = E ( m , H ) ⊕ H ⊕ m = E ( H ⊕ m , m ) ⊕ m Other natural variants are insecure :
h ( H , m ) = E ( m , H ) ⊕ m h(H, m) = E(m, H) \oplus m h ( H , m ) = E ( m , H ) ⊕ m SHA256:
Merkle-Damgrad funciton
Daives-Meyer Comporession
SHACAL-2 block cipher.
Choose a random 2000-bit prime number, p p p 1 ≤ u , v ≤ p 1 \le u, v \le p 1 ≤ u , v ≤ p m , h ∈ { 0 , . . . p − 1 } m, h \in \{0, ... p - 1\} m , h ∈ { 0 , ... p − 1 } h ( H , m ) = u H ⋅ v m ( m o d p ) h(H, m) = u^H \cdot v^m (\mod p) h ( H , m ) = u H ⋅ v m ( mod p ) slow .
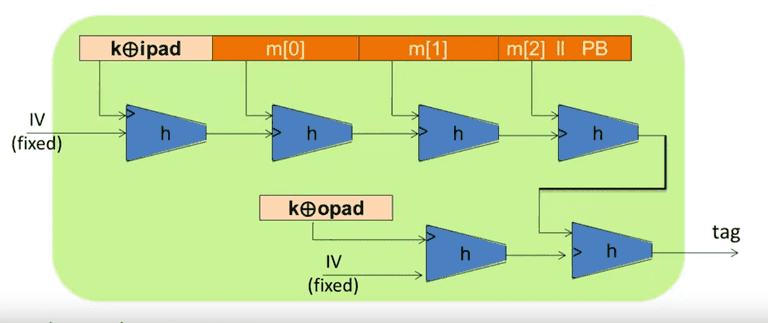
HMAC
S ( k , m ) = H ( k ⊕ o p a d , H ( k ⊕ i p a d ∣ ∣ m ) ) S(k,m) = H(k \oplus opad, H(k \oplus ipad || m)) S ( k , m ) = H ( k ⊕ o p a d , H ( k ⊕ i p a d ∣∣ m ))
HMAC