Block Cipher
Block Cipher
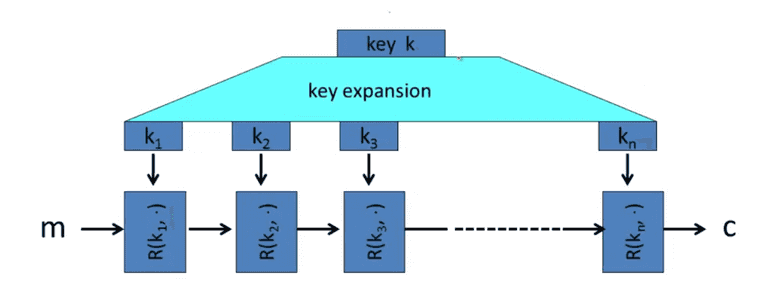
Such as 3DES, and AES. The idea is to use PRG to expand the k, and encrypt the message m in various rounds to get encrypted c.
PRP and PRF
The pseudo random function PRF is defined:
The pseudo random permutation is defined:
PRP also requires the E is one-to-one, and exists efficient inversion algorithm D.
The PRF is secure if it non-distinguishable from a true random function.
Data Encryption Standard(DES)
Based on the Feistel Network: Given arbitrary functions, , the forward functions are:
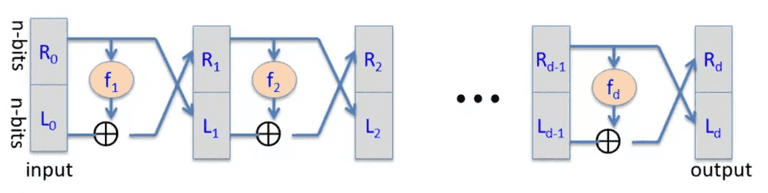
The has to be secure PRF, with independent keys to get secure DES.
DO NOT use linear function for S-box, otherwise, DES becomes linear, too.
The weakness of DES is the key is only 56bit.
- COPACOBANA takes 7 days with 10K$, 120 FPGA to crack in 2006.
Triple-DES
Define 3E: as:
It use E, D, E thus 3DES is degrades to DES if for backward compatibility.
What is the problem of double DES?
We can use “meet-in-the-middle attack.“:
- Build a table for all entries, and sort on the second column.
- For all possible to decrypt the , and lookup the table.
The time complexity is the .
DESX
Define EX:
The key-length is bits, but attack time is .
Attacks on Block Ciphers
- Side channel attacks
- Fault attacks
- Linear and differential attacks
Give many pairs, if the subset of message bits xored compared with subset of ct bits xored, and show some linear relationship, , for DES, a tiny bit of linearity is leads to: Roughly speaking: can find 14 key “bits” in time .
We can then brutal force for 42 bits, and the total time is .
Advanced Encrypt Standard(AES)
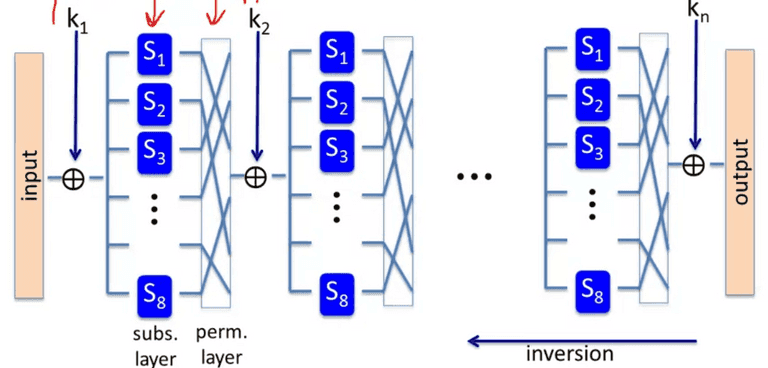
Use subs-perm network:
The perm network MUST be invertible.
AES-128
10 rounds, with 11 keys expanded from key(16 bytes -> 176 bytes.)
Each round the input is hashed to 4x4 matrix, and use ByteSub, ShiftRow, MixColumn(except the last round), and output with the round key.
The AES allows code size/performance trade-off.
Intel Westmere supports instructor, 14x speedup in OpenSSL.
aesenc,aesenclastfor AES round.aeskeygenassistperform AES key expansion.
Key Recovery attack: 4x better than brutal force.
Block Ciphers from PRGs
GGM PRF can recursively invoke the PRG to extend 1-bit PRG. With Luby-Rackoff theorem: PRG -> GGM PRF -> PRP, aka block cipher
It is considerably slow as each round only generate 1-bit!
Block cipher is essentially a PRP. It is regarded as secure if the PRF is secure. A concrete example about AES: Secure PRP is also a secure PRF if is sufficient large, with q-queries:
Electric Code Book, ECB encrypt the same message as same CT, which leaks the information to the adversary.
Semantic Security: the adversary should not distinguish two messages with same length encrypted by the cipher.
We can use AES to generate OTP for stream encryption.
Use Block Cipher with many-time key
Chosen-plaintext attack(CPA)
The adversary gains advantage 1 if he can detect the same message are encrypted to the same PT, that breaks the semantic security!
- Randomized encryption: add random bits, aka salt, to the message on the expense of longer CT size.
- nonce-based encryption: nonce is public, can use counter or random. The
EandDinclude the nonce.
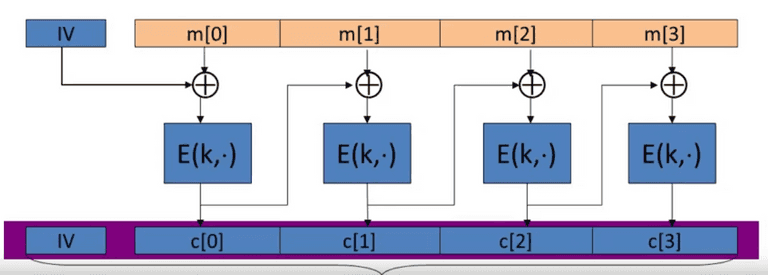
Cipher Block Chaining(CBC)
CBC with random Initial Vector(IV). IV is the size the block. The output is fed into the next block.
The chosen-plain text attack against CBC is: CBC is only secure if .
For AES, if the threshold is , , then . So after AES blocks, MUST change key.
3DES: .
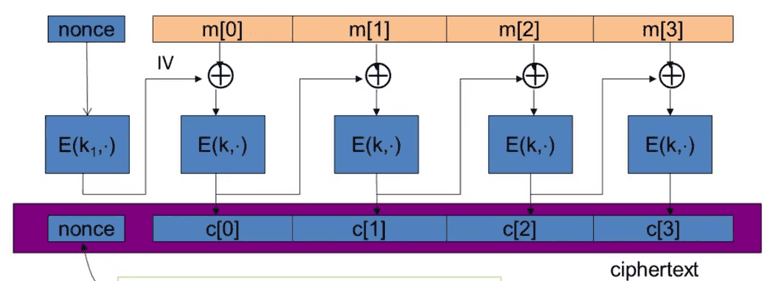
nonce-based CBC
The IV MUST be random to ensure CPA-secure!
Use key space , nonce is not random, but unique. It is crucial to encrypt nonce with , otherwise, CBC is not CBA-secure!
CBC use padding, for n byte pad, just use padding with byte n. The decryptor will remove last n byte. For no-padding, add a block with byte 16 .
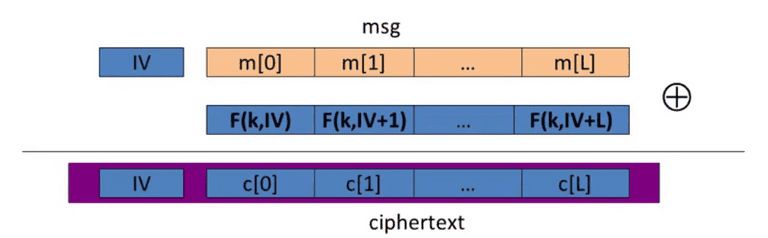
Randomized Counter Mode(CTR)
IV is a counter, the F is a secure PRF, — completely parallelizable.
The q-query adversary A attacking : Better than CBC!
The block ciphers can be interpreted as PRP or PRF.