Authenticated Encryption
Combine confidentiality and integrity to for encryption secure against tampering.
The attacker can divert the package by update the IV, and let the server to decrypt the message for him! Without integrity, no confidentiality is protected.
Chosen Ciphertext Attack, thereafter CCA: The attacker craft the cipher text, such as and encrypted data, such as , and observe the ack from the server, it can find the D: .
Authenticated Encryption
A cipher(E, D) where:
Note: . It is claimed to be authenticated encryption(AE) if it is:
- semantically secure under CPA, aka negligible information about the plaintext can be feasibly extracted from the ciphertext
- has ciphertext integrity, aka hacker cannot craft arbitrary ciphertext not from intercepted ciphertext.
Chosen Ciphertext Security
Adversary’s power: both CPA and CCA Adversary’s goal: break semantic security
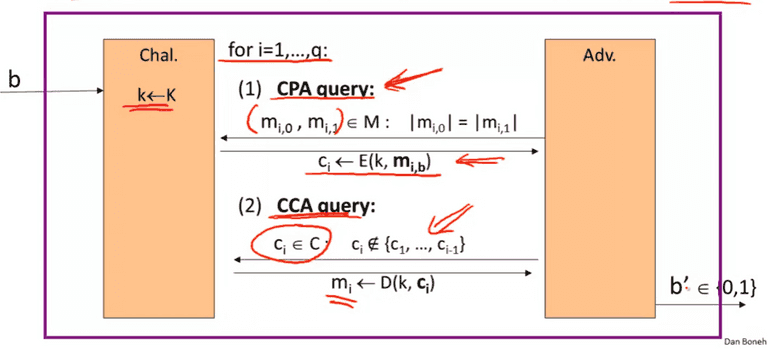
The goal is for Adv. to determined whether it is in experiment 0 or 1. If the probably is “negligible”, we call E is CCA secure.
AE is CCA secure.
For any q-query eff. A, there exists eff. adversaries , s.t:
However:
- does not prevent replay attacks.
- does not prevent side channels attack.
Constructions form ciphers and MACs.
Assume we have encryption key: and MAC key, :
- SSL: , aka MAC-then-encrypt.
- IPSec: , aka encrypt-then-mac ✅
- SSH: , aka encrypt, then MAC on the message, enc-and-mac. ⛔
MAC-then-encrypt: when E,D is rand-CTR mode or rand CBC, then AE. For rand-CTR mode, one-time MAC is sufficient.
Standards
- Galois/Counter Mode, GCM, CTR mode encryption then CW-MAC.
- CCM: CBC-MAC then CTR mode encryption. All based on AES.
- EAX: CTR mode encryption then CMAC.
All are nonce-based, aka (key, nonce) cannot be repeated. All support AEAD(authenticated, encrypted with associated data)
Direct construction from PRP, aka OCB:
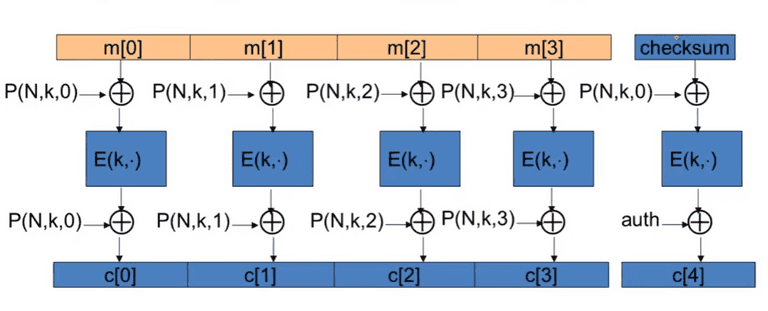
- Parallelizable
- Use , for Nonce, key, and counter.
It is not widely-used due to the patent.
TLS 1.2
Use MAC-then-encrypt scheme with CTR to avoid replay attack.
Prior to TLS1.1
- BEAST attack: IV for CBC is predictable.
- Padding Oracle: leaking information about plaintext during encryption due to illegal padding.
CRC is not secure as the CRC is linear: . For WEP, attacker can modify the ciphertext with , then use to get a valid CRC checksum!
Before OpenSSL 0.9.7a, attacker can launch timing attack to differentiate the padding error vs. decryption error.
Key Derivation
A single uniform source key, SK to generate many keys with KDF(Key Derivation Function):
Use from HMAC.
The password-based source key does not sufficient entropy. DO NOT use HKDF, use PKCS#5, aka PBKDF1: with slow hash function.
Deterministic Encryption
The determined encryption may not be CPA secure due to that the same messages yield same ciphertexts.
The solution is to never encrypt the same message twice:
- use primary key for uniqueness.
CBC with fixed IV is not deterministic CPA secure.
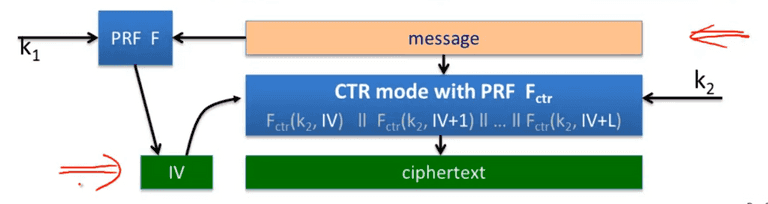
Synthetic IV (SIV)
Let (E, D) be a CPA-secure encryption, and be a secure PRF, Define
The det. CPA security + ciphertext integrity DAE: deterministic authenticated encryption.
Decryption:
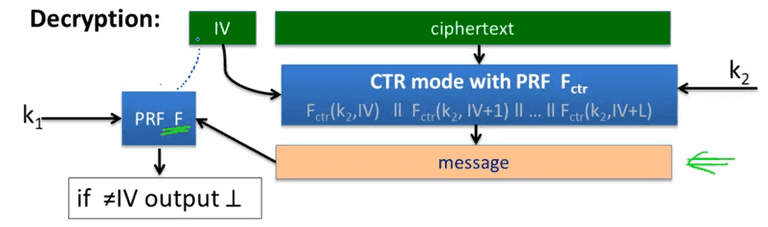
Then use message with PRF to validate the IV.
Thm: if F is secure PRF, and CTR from is CPA secure, then SIV-CTR from F, provides DAE.
Use PRP
Let (E, D) be a securfe PRP. . (E, D) is semantical secure under det. CPA.
Can be 2x slower than SIV.
The Det. Authenticated Enc:
- Just appends n(e.g 80) bits zeros
- Verify the decrypted text has n bits zeros.
The idea is to invert the permutation function to get the last n bits with zero. If the PRF is secure, which means the probability to achieve this goal is . The encode is secure if is negligible.
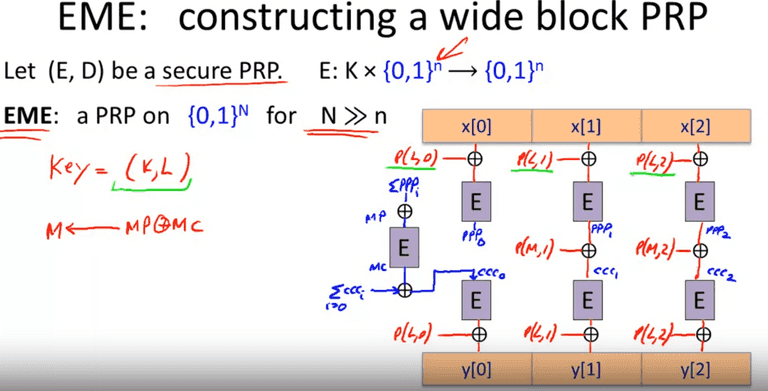
Tweakable Encryption
Disk encryption:
- M = C
- Must be deterministic encryption.
Thus the encryption is a PRP. We can construct the PRP directly from the key: , is an invertible function on X, indistinguishable from random. More concretely using the sector number as T(Tweak).
XTS tweakable block cipher
Let (E, D) be a secure PRP. Define XTS:
and , so we can encrypt
Formatting Preserving Encryption
CC format: bbbb bbnn nnnn nnnc (roughly 42 bits)
- 6 digit: issuer ID
- last digit checksum.
Pick , in our case t = 42. Use Luby-Rackoff with .
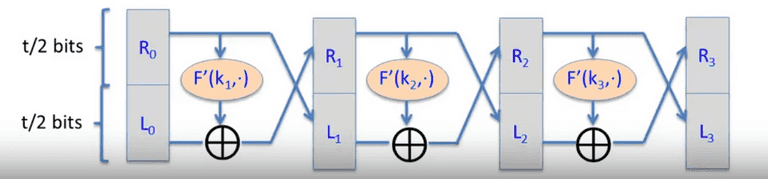
Better to use 7 rounds.
Given (E, D): , we build (E’, D’): Repeat the until .