Public Key Encryption

Define the (G, E, D):

• G: randomize algorithm to generate key pairs (pk, sk).
• E(pk, m) takes $m\in M$ and output $c\in C$.
• D(sk, c) takes $c \in C$ and outputs $m \in M$ or $\perp$.

Define Trapdoor function(TDF)

• G: randomize algorithm to generate key pairs (pk, sk).
• $F(pk, \cdot)$ maps $X \to Y$.
• $F^{-1}(pk, \cdot)$ maps $Y \to X$, that inverts $F(pk, \cdot)$.

TDF is secure if $F(pk, \cdot)$ can be evaluated, but cannot be inverted without sk.

Construct

Use secure TDF, symmetric auth encryption defined over (K, M, C) and hash function $H \to K$(also called random oracle):

E(pk, m):

• $x \leftarrow X$, $y \leftarrow F(pk, x)$
• $k \leftarrow H(x)$, $c \leftarrow E(k, m)$
• output (y, c)

D(sk, (y, c))

• $x \leftarrow F^{-1}(sk, y)$
• $k \leftarrow H(x)$, $m \leftarrow D(k, c)$
• output m

Never use TDF to encrypt the message directly!

RSA Trapdoor permutation

$G$: choose random $p, q \approx 1024 bits$, set $N = p \cdot q$. choose integers $e, d$, such that $e \cdot d = 1 (mod \ \phi(N))$. output $pk = (N, e)$, $sk = (N, d)$.

$F(pk, x): RSA(x) = x^e \in Z_n$ $F^{-1}(sk, y) = y^d = RSA(x)^d = x^{ed} = x^{k\phi(N) + 1} = (x^{\phi(N)})^k \cdot x = x$

E, D: symmetric encryption. H: $Z_N \to K$

$E(pk, m)$:

1. choose random x in $Z_N$.
2. $y \leftarrow RSA(x) = x^e, k \leftarrow H(x)$
3. output (y, E(k, m))

$D(sk, (y, c))$: output $D(H(RSA^{-1}(y)), c) \to m$.

If we use RSA directly to exchange the session key, $k$, the server send the public key, (e, N), and the client returns $c = RSA(k)$.

Assume $k = k_1, \cdot k_2$, thus $c = k_1^e \cdot k_2^e \to c/k_1^e = k_2^e$, if k is 64 bit, the chance for $k_1, k_2 < 2^34$ is roughly 20%. The attacker can build a lookup table to enumerate $k_1, k_2$ from 1 to $2^{34}$ for a mid-way attack!

PKCS1

The PKCS1 v1.5 mode 2, used in HTTPS:

The random pad does not contain FF.

Bleichenbacher 1998 attack:

• choose $r \in Z_N$, computer $c\prime \leftarrow r^e \cdot c = (r \cdot PKCS1(m))^e$
• send c’ to web server.l The attacker can recover m with many trials. / HTTPS Defence(RFC 5246) treats the incorrect formated messages indistinguishable from correctly formatted RSA blocks.

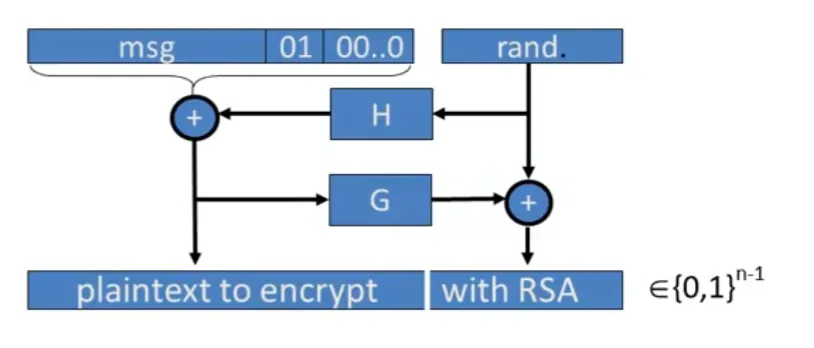
PKCS1 v2.0: OAEP

Assume H, and G are random oracles, typically use SHA-256

RSA security analysis

Use $d \approx 2^{128}$:

• Weiner ‘87: if $d < N^{0.25}$, RSA is insecure.
• BD’98: if $d < N^{0.292}$, RSA is insecure. $0.292 = 1 - \frac{1}{\sqrt{2}}$

Wiener’s attack

$e \cdot d = 1 (\ mod\ \phi(N)) \to e \cdot d = k \cdot \phi(N) + 1$. thus : $|\frac{e}{\phi(N)} - \frac{k}{d}| = \frac{1}{d\cdot \phi(N)} < \frac{1}{\sqrt{N}}$. $|N -\phi(N)| \le p + q \le 3 \sqrt{N}$.

Also:

Fault Attack

When decrypting RSA, we can gain 4x speedup with:

• Decrypt mod p $x_p = c^d \in Zp$
• Decrypt mod q $x_q = c^d \in Z_p$ then combine them to get $x = c^d \in Z_N$.

Suppose error occurs when computing $x_q$, but not in $x_p$, the output is $x\prime$, and $gcd((x\prime)^e -c, N) = p$, thus we can recover p.

Bad random generate may get the same p, different q, then $gcd(N_1, N_2) = p$ to recover the p.

ElGamal Public-key System

We can use Diffie-Hellman protocol to build public key. Intuitively: Use A as public key: $A = g^a$ Bob sends B=$g^b$ || message encrypted with $k = g^{ab}$.

Key generator:

• choose random geneator g in G, and random a in $Z_n$.
• output sk = a, pk = (g, $h=g^a$). H: $G^2 \to K$, a hash function.

Encryption: $E(pk=(g, h), m)$:

• $b \in Z_N, u \leftarrow g^b, v \leftarrow h^b$
• $k \leftarrow H(u, v), c \leftarrow E(k, m)$
• output (u, c)

Decryption:

• $v \leftarrow u^a$
• $k \leftarrow H(u, v), m \leftarrow D(k, c)$
• output m

Encryption is 3x expensive as decryption, while RSA decryption is more expensive.

Twin ElGamal, use $(a_1, a_2) \in Z_N$ for the private keys.

Review