Message Authentication Code
This week we focuses on the data integrity, Message Authentication Codes.
Define: MAC I=(S,V) defined over (K,M,T):
- S(k,m) outputs t in T.
- V(k,m,t) output ‘yes’ or ‘no’
S stands for signing, V stands for verification.
Attacker can give Alice m1,...mq, to get ti←S(k,mi). The goal is to produce some new valid message/tag pairs (m, t), aka existential forgery, such that:
(m,t)∈/{(m1,t1),...,(mq,tq)}
The MAC is secure if attacker cannot generate new (m, t), even for existing message, mi. Or more formally: AdvMAC[A,I]=Pr[Chal.outputs1] is negligible.
The error bound of PRF is AdvMAC[A,IF]≤AdvPRF[B,F]+1/∣Y∣
The IF is secure as long as ∣Y∣ is large enough.
Extend AES(16 bytes) from Small-MAC to Big-MAC:
- CBC-MAC, ANSI X9.9, FIPS 186-3
- HMAC, SSL, IPSec, SSH.
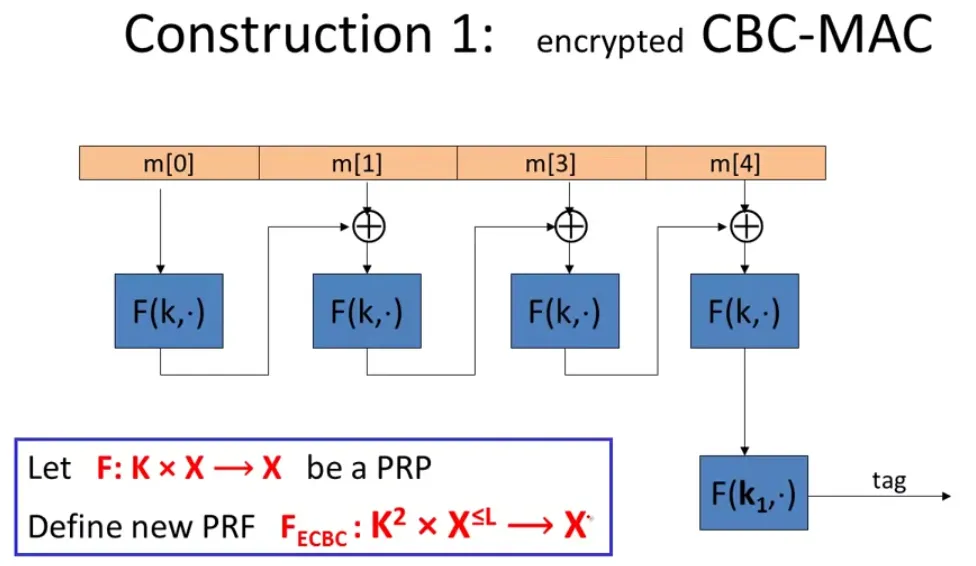
It is important to use independent k1 to encrypt the raw CBC output.
For raw CBC, the attacker can
- choose one block message m, to get t=F(k,m).
- then for 2-block message (m,t⊕m) , the MAC is t!
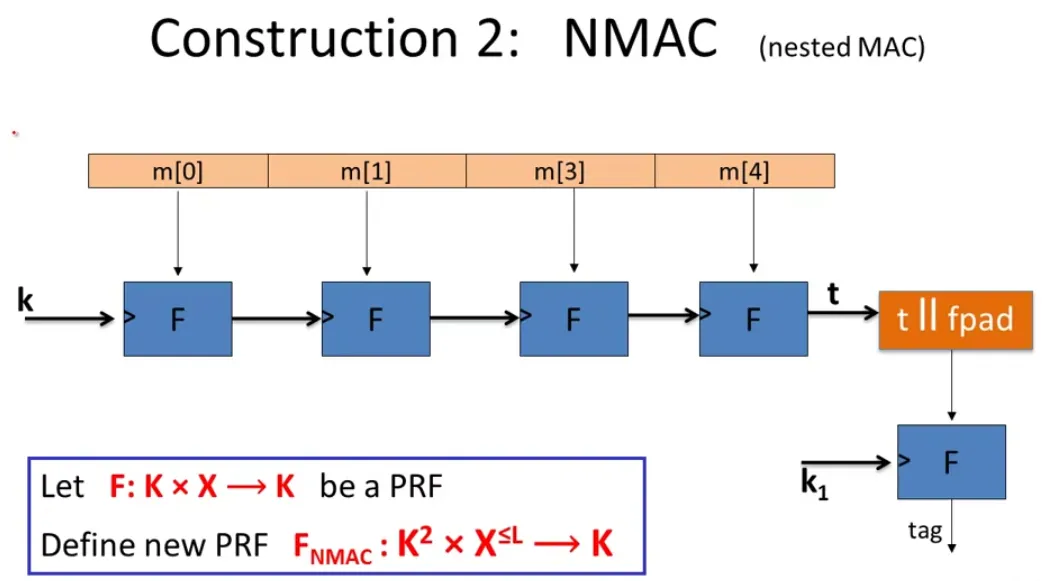
Also the independent k1 encrypt the output of cascade MAC to make it secure.
AdvPRF[A,FECBC]AdvPRF[A,FNMAC]≤AdvPRF[B,F]+∣X∣2q2≤q⋅L⋅AdvPRF[B,F]+2∣K∣q2
We need to rotate keys for after ∣X∣1/2 messages with ECBC-MAC or ∣K∣1/2 for NMAC.
Once we find a hash collision, we can extend any arbitrary block to mount forgery attack.
Padding MUST be invertible to prevent forgery.
ISO: padding with 10000, 1 indicates the beginning of the padding. In case message has a clear cut, just append a dummy block.
CMAC uses k1 for padding block, and k2 for no-padding block to resolve the ambiguity. It is as safe as CBC-MAC, and standardized by NIST.
Parallel MAC
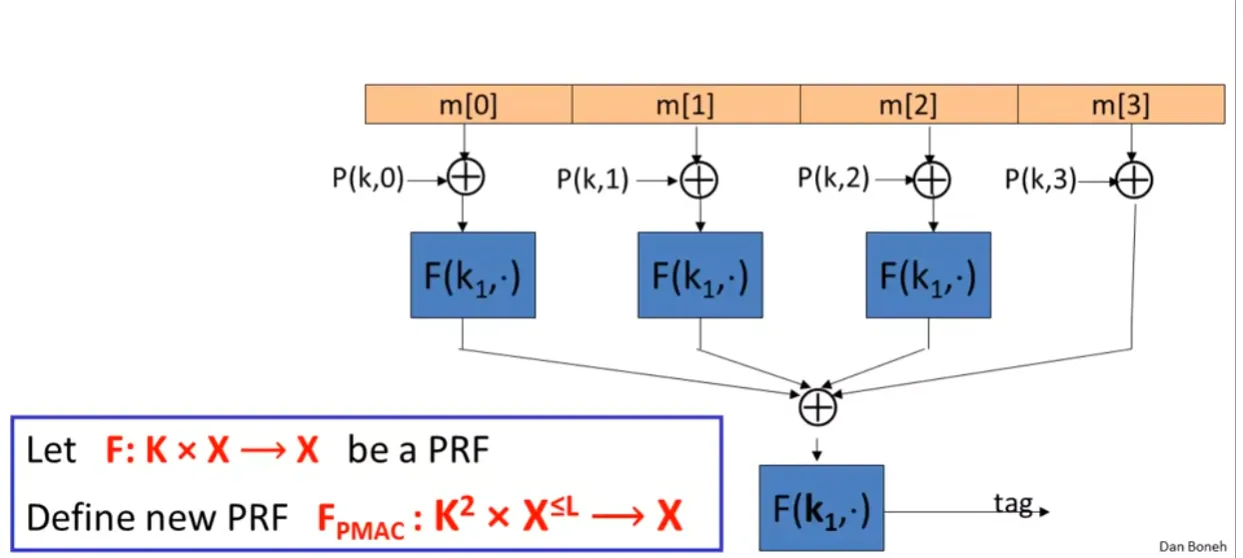
The P(k,i) enforce the block order, such k×i. The padding use similar technical as CMAC.
AdvPRF[A,FPMAC]≤AdvPRF[B,F]+∣X∣2q2L2
It is easy to replace one specific block, and compute the MAC without recomputing everything.
Kind of like OTP, pick key, (k,a)∈{1,...q}2 where q is a large prime number such as (q=2128+51), and break the message to blocks, (m[1],...,m[L]):
S(key,msg)=(Pmsg(k)+a)modq
where Pmsg(x)=m[L]⋅xL+...+m[1]⋅x, aka a polynomial of L.
Cater-Wegman MAC:
CW((k1,k2),m)=(r,F(k1,r)⊕S(k2,m))
for F be a secure PRF, for r is random chosen: r←{0,1}n. The verification is:
V(k2,m,F(k1,r)⊕t)).
A function H is collision resistant if for efficient algorithms, the chance to fine the same hash is negligible.
Let I=(S,V) be a MAC for short message over (K,M,T),
Let H: Mbig→M
Def: Ibig=(Sbig,Vbig) over (K,Mbig,T) as:
Sbig(k,m)=S(k,H(m));Vbig(k,m,t)=V(k,H(m),t)
Thm: If I is a secure MAC and H is collision resistant, then Ibig is a secure MAC.
Let H:M→{0,1}n be a hash function (∣M∣≫2n)
We can find a collision in time O(2n/2) thanks to the birthday paradox:
Let r1,...,rn∈{1,..,B} be independent uniformly distributed integers.
when n=1.2×B1/2 then Pr[∃i=j:ri=rj]≥21
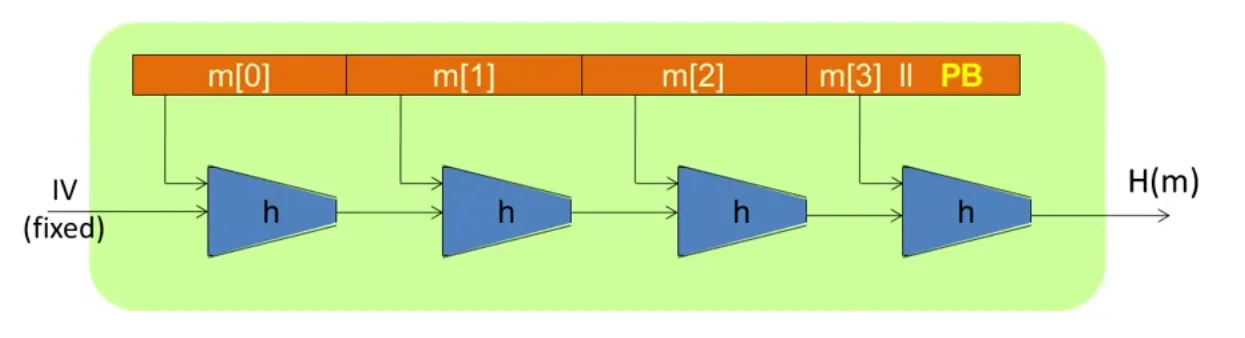
Given h:T×X→T, we obtain H:X≤L→T. So we can build a collision resistant function for larger message.
E:K×{0,1}n→{0,1}n a block cipher: h(H,m)=E(m,H)⊕H.
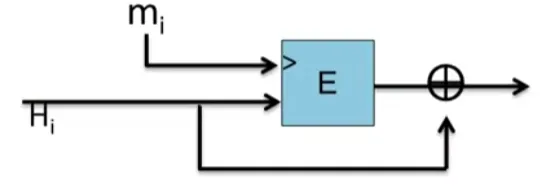 Suppose E is an ideal cipher, finding a collision of h(H,m)=h(H′,m′) takes O(2n/2) evaluations of (E, D).
Suppose E is an ideal cipher, finding a collision of h(H,m)=h(H′,m′) takes O(2n/2) evaluations of (E, D).
Miyaguchi-Preneel:
h(H,m)h(H,m)=E(m,H)⊕H⊕m=E(H⊕m,m)⊕m
Other natural variants are insecure:
h(H,m)=E(m,H)⊕m
SHA256:
- Merkle-Damgrad funciton
- Daives-Meyer Comporession
- SHACAL-2 block cipher.
Choose a random 2000-bit prime number, p and random 1≤u,v≤p. For m,h∈{0,...p−1}, define h(H,m)=uH⋅vm(modp). is provable secure, but slow.
S(k,m)=H(k⊕opad,H(k⊕ipad∣∣m))
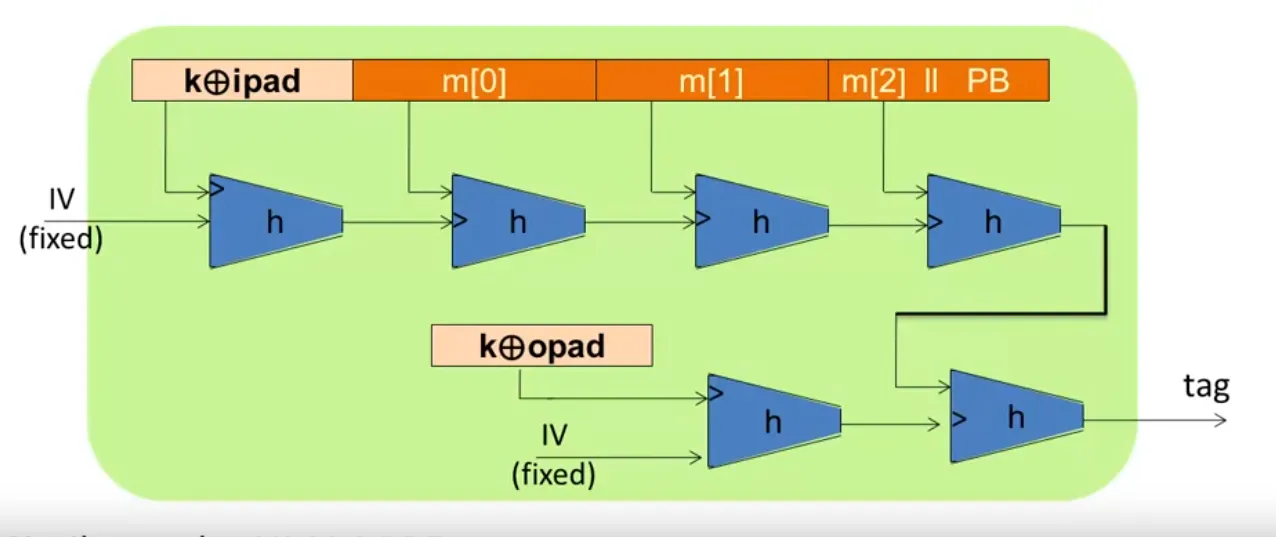




 Suppose E is an ideal cipher, finding a collision of takes evaluations of (E, D).
Suppose E is an ideal cipher, finding a collision of takes evaluations of (E, D).