Key Exchange

How could Alice, Bob, and Christ to exchange keys safely? Use trusted third party, (TTP)

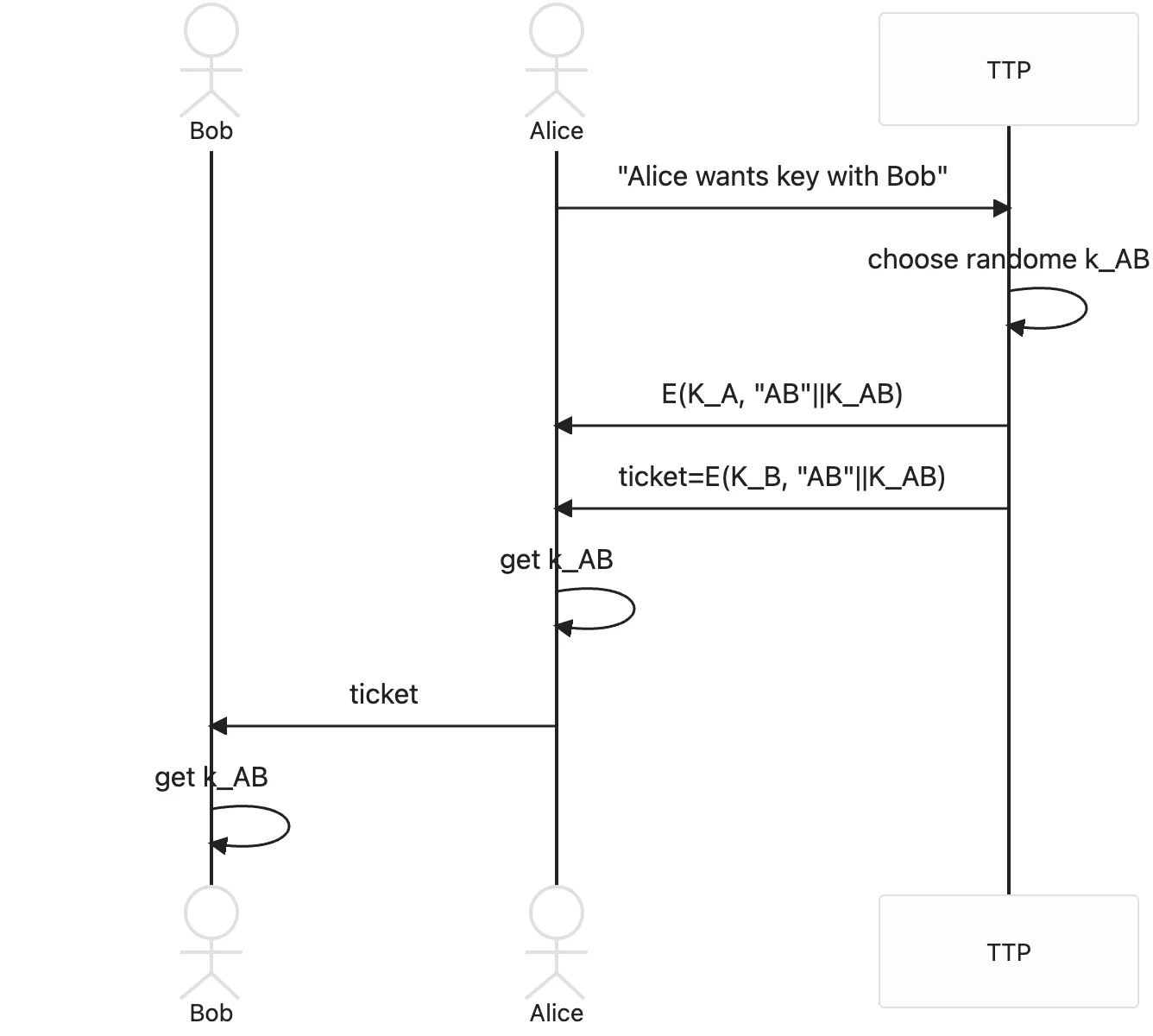
Basics of Kerbose. Insecure against active attacks, such as replay attacks.

Decentralized key exchanges:

• Merkel (1974)
• Diffe-Hellman (1976)
• RSA (1977)
• ID-based enc. (BF 2001)
• Functional enc. (BSW 2011)

Merkel Puzzles

E(k, m) is a symmetric cipher with $k \in \{0,1\}^{128}$, define puzzle(P) = E(P, “message”), where $P = 0^{96}||b_1,... b_{32}$.

• Alice prepare $2^{32}$ puzzles, set $puzzle_i \leftarrow E(0^{96}|| Pi, Puzzle \#x_j || k_j)$, and send all of them to Bob.
• Bob choose a random puzzle, solve it, obtain $(x_j, k_j)$, and send $x_j$ to Alice.

The eavesdropper needs to to solve $2^{32}$ puzzles to figure out the $k_j$ specified by $x_j$, so the time complexity is $O(n^2)$.

Quadratic gap is possible if we treat ciper as a black box oracle.

Diffie-Hellman

Fix a large prime $p$, (e.g 600 digits, $\{0, 1\}^{2000}$). Fix an integer g such that $0 < g \le p$.

Alice choose random a such $a < p$, Bob choose random b such as $b < p$.

• Alice -> Bob: $A \leftarrow g^a (mod\ p)$.
• Bob -> Alice: $B \leftarrow g^b (mod \ p)$

Then, they can get the secret:

• Alice: $B^a (mod \ p) = g^{ab}$
• Bob: $A^b (mod \ p) = g^{ab}$

the mod p is the number space $Z_p$, see Number Theory below.

Best known algorithm to solve DH problem, arithmetic modular function, is roughly $exp(O(\sqrt[3]{n}))$, thus

Alternatively, we can use elliptic curve to decrease the size, see above.

The Diffie-Hellman is insure against man-in-the-middle attack.

Public-Key Encryption

Define the (G, E, D):

• G: randomize algorithm to generate key pairs (pk, sk).
• E(pk, m) takes $m\in M$ and output $c\in C$.
• D(sk, c) takes $c \in C$ and outputs $m \in M$ or $\perp$.

Number Theory

Notion: $N$ is a positive number, $p$ is a positive prime number, and $Z_N = \{0, 1, ..., N-1\}$.

The modular arithmetic: $x \cdot (y + z) = x \cdot y + x \cdot z$.

For all integers. $x, y$ there exists integers. $a, b$ such that $a \cdot x + b \cdot y = gcd(x, y)$.

Inverse of x in $Z_N$ is an element in $Z_N$, aka $x \cdot y = 1$ in $Z_N$. x in $Z_N$ has an inverse if and only if $gcd(x, N) = 1$.

Proof: $\exists a, b: a \cdot x + b \cdot N = a \cdot x = 1$. thus $x^{-1} = a$ in $Z_N$.

$Z^*_N = \{ x \in Z_N: gcd(x, N) = 1\}$

Fermat’s theorem

Let p be a prime, $\forall x \in Z^*_p: x^{p -1} = 1$

To generate large random prime:

1. Choose a a random integer $p \in [2^{1024}, 2^{1025} -1]$
2. test if $2^{p-1} = 1$ in $Z_p$.
3. If so, output p. Otherwise, go to step 1 The chance that p is not prime < $2^{-60}$.

Euler Theory

$(Z_p)^*$ is a cyclic group, that is $\exists g\in (Z_p)^*$, such that $\{1, g, g^2, ... g^{p-2}\} = (Z_p)^*$. g is called a generator of $(Z_p)^*$.

Given $g \in (Zp)^*$, the set of $\{1, g, g^2, ... \}$ is called the group generated by g, denoted as <g>. The order of $g \in (Z_p)^*$ is the size of $<g>$: $ord_p(g) = |<g>| = (smallest\ a > 0, s.t.\ g^a = 1 \in Z_p)$ Thm Lagranage: $\forall g \in (Z_p)^*: ord_p(g)\ divides\ (p -1)$.

Euler’s $\phi$ function

for an integer $N$, define $\phi(N) = |(Z_N)^*|$. Examples:

• $\phi(p) = p - 1$.
• For $N = p \cdot q: \phi(N) = N - p - q + 1 = (p -1)(q - 1)$.

Euler’s theorem: $\forall x \in (Z_N)^*: x^{\phi(N)} = 1$.

Modular e’th roots

When does $c^{1/e}$ in $Z_p$ exists? Suppose $gcd(e, p - 1) = 1$, for all c in $(Z_p)^*$, $c^{1/e}$ in $Z_p$ exists. let $d = e^{-1}$ in $Z_{p-1}$ , $c^{1/e} = c^d$ in $Z_p$.

x in $(Z_p)^*$ is Quadratic Residue, aka Q.R, if and only if $x^{(p - 1)/2} = 1$ in $Z_p$. p is odd prime.

Arithmetic algorithms

How to support 2048 bit number arithmetic operations? Karatsuba 1960: use 3 mults to achieve $O(n^{\log_2{3}}) = O(n^{1.585})$.

Define: $Dlog_g(g^x) = x$.

DLOG is hard in G if for all efficient algorithm A: $Pr_{g \leftarrow G, x \leftarrow Z_q} [A(G, q, g, g^x) = x]$ is negligible. such as:

• $(Z_p)^*$ for large p, see Diffle-Hellman
• Elliptic curve group mod p

Collision resistance

For a group G, q = |G| be a prime, choose generate g, h of G, for $x, y \in \{1, ... q\}$, define $H(x, y) = g^x \cdot g^y$ in G. Finding collision for $H$ is as hard as computing $DLOG_g(h)$.