LFU Cache in Python

Dec 27, 2016 python algorithm interview

In the last post, we explore the LRU cache implementation with OrderedDict, now comes to the new challenge: can you implement a Least Frequently Used (LFU) cache with the similar constraints?

$O(1)$ time complexity for read(get) and write(set) operations
if the cache grows out of the capacity limit, the least frequently used item is invalidated. If there exists a tie, the least recently accessed key will be evicted¹.

Track the accesses with doubly linked list

It is pretty obvious that we MUST use dict as the internal data store to achieve the $O(1)$ complexity for the data access, and somehow keep cache items sorted with the access frequency all the time. Otherwise, the data eviction has to iterate all cache items(aka $O(n)$ complexity) to find the least frequently used.

Inspired by the LRU cache implementation, the accesses frequency is tracked with a doubly linked list (see here for the linked list operations details, such as dll_append). Without loss of generality, we store all the item (key, value) pair and an access counter sorted by the number of accesses in the descending order.

For any operations with cache hits, the node is moved towards the list head to maintain the order.
For set operation with a cache miss, the tail node will be evicted if the cache reaches capacity limit. A new node is appended then moved accordingly.

class LFUCache(object):
    def __init__(self, capacity, update_func):
        self.capacity = capacity
        self.update_freq = update_func
        self.cache = dict()
        self.head = dll_init()

    def set(self, key, value):
        # special case for capacity <= 0
        if self.capacity <= 0:
            return

        # Does the key exist in the cache?
        node = self.cache.get(key)
        if node:
            key, _, counter = node[2]
            node[2] = (key, value, counter)
            self.update_freq(node, self.head)
            return

        # Remove the LRU key if exceeding the capacity
        if len(self.cache) >= self.capacity:
            # remove the last element
            node = dll_remove(self.head[0])
            self.cache.pop(node[2][0])

        # Append to the end of double-linked list
        node = dll_append(self.head, (key, value, 0))
        self.cache[key] = node
        self.update_freq(node, self.head)

    def get(self, key):
        node = self.cache.get(key)
        if node is None:
            return -1
        self.update_freq(node, self.head)
        return node[2][1]

The preliminary profiling shows that the majority CPU time is spent on the linked list reordering, so the LFUCache.update_freq method is deliberately extracted externally to test the different policies. For example, the first attempt takes a bubble-sortesque approach:

If the access counter of the node is no less than the its precedence, swap them.
Repeat the step 1 until the condition no longer stands.

def bubble_update(node, head):
    # Update the access counter of the node, then bubble it up
    # by swapping the node with its precedence.
    # update access count for node
    prev, next_, (key, value, counter) = node
    counter += 1
    node[2] = (key, value, counter)
    while(prev is not head and prev[2][2] <= counter):
        # swap prev and node
        prev2 = prev[0]
        prev2[1] = node

        node[0] = prev2
        node[1] = prev

        prev[0] = node
        prev[1] = next_

        next_[0] = prev

        # reset all variables for the next loop
        next_ = prev
        prev = prev2
        prev2 = prev[0]

In a synthetic benchmark, 7941 get, 12558 set ops on 2K-entry cache take more than 30 seconds in the profiling. If the cache is so ridiculously slow, why bother?

I then found an optimization with a insert-sortesque approach to avoid the expensive swap operation:

Iterate the precedences of the node until the access counter of the precedence, aka pivot, is larger than the node.
Insert the node after the pivot.

def insert_update(node, head):
    '''Update the access counter, then find the pivot from the
    tail of the linked list, insert the node AFTER the pivot.'''
    # update access count for node
    pivot, _, (key, value, counter) = node
    counter += 1
    node[2] = (key, value, counter)
    while(pivot is not head and pivot[2][2] <= counter):
        pivot = pivot[0]

    # Insert the node AFTER the pivot
    if pivot is not node[0]:
        # remove the node from the linked list
        dll_remove(node)
        # insert after the pivot
        node[1] = pivot[1]
        node[0] = pivot
        pivot[1][0] = node
        pivot[1] = node

This performs significantly better, 8.45s in the synthetic benchmark with profiling enabled, but still way too slow. The profiling shows that 99.4% CPU time is spent on the doubly linked list traversal, and we do it linearly, anyway we can leverage the sorted linked list to make it faster?

Put it in the bucket

The lfu paper presents a neat solution to address the performance issue: the single doubly linked list is segmented to multiple buckets, the node with the same access counter are put into the same bucket in the order of recentness. When the access counter is updated, we can simply pop the node from the current bucket, and place it to the new bucket. Illustrated as below:

I take a simplified detour to explore the idea but avoiding the hustle of wrangling doubly doubly linked list: a lookup table is used to map the access counter to the bucket. This may incur $O(n)$ complexity of the key eviction in the worst case; but it turns out that it performs very well, — 0.35s with profiling enabled, a 24x performance boost.

from collections import defaultdict


class LFUCache2(object):
    def __init__(self, capacity, *args):
        self.capacity = capacity
        self.bucket_lut = defaultdict(dll_init)
        self.cache = dict()

    def remove_node(self, node):
        # Remove the node from the cache and also the bucket
        _, _, (key, value, counter) = node
        dll_remove(node)
        self.cache.pop(key)
        # clean up the freq_head if it is empty
        bucket = self.bucket_lut[counter]
        if bucket[1] is bucket:
            self.bucket_lut.pop(counter)

    def add_node(self, data):
        # Create a node to host the data, add it to cache and
        # append to the bucket.
        bucket = self.bucket_lut[data[2]]
        node = dll_append(bucket, data)
        self.cache[data[0]] = node

    def set(self, key, value):
        # special case for capacity <= 0
        if self.capacity <= 0:
            return

        # Does the key exist in the cache?
        node = self.cache.get(key)
        if node:
            # Update the value and counter
            counter = node[2][2]
            self.remove_node(node)
            self.add_node((key, value, counter + 1))
            return

        if len(self.cache) >= self.capacity:
            # Remove the least used, least recently accessed
            min_counter = min(self.bucket_lut.keys())
            bucket = self.bucket_lut[min_counter]
            self.remove_node(bucket[1])

        self.add_node((key, value, 1))

    def get(self, key):
        node = self.cache.get(key)
        if node is None:
            return -1

        key, value, counter = node[2]
        self.remove_node(node)
        self.add_node((key, value, counter + 1))
        return value

It took many hours to get the doubly doubly linked list solution right due to its complexity. I had to use the namedtuple to sort out the list index. And it just performed as well as the simplified version.

from collections import namedtuple

# head points to the doubly linked list of Node
Bucket = namedtuple('Bucket', ['counter', 'head'])
# item caches a reference to the bucket_node for quick accss the next bucket
Item = namedtuple('Item',['key', 'value', 'bucket_node'])

class LFUCache3(object):
    def __init__(self, capacity, *args):
        self.capacity = capacity
        self.bucket_head = dll_init()
        self.cache = dict()

    def remove_node(self, node):
        item = node[2]
        self.cache.pop(item.key)   # remove from cache
        dll_remove(node)           # remove node from the bucket

        bucket = item.bucket_node[2]
        if bucket.head[1] is bucket.head:
            # remove the bucket if empty
            dll_remove(item.bucket_node)

    def add_node(self, key, value, original_bucket_node):
        '''Add the (key, value) content pulled from orginal_bucket_node
        to a new bucket'''
        counter = 0 if original_bucket_node is self.bucket_head \
            else (original_bucket_node[2].counter)
        next_bucket_node = original_bucket_node[1]

        if next_bucket_node is self.bucket_head:
            # No bucket(counter + k) exists, append a new bucket(counter + 1)
            bucket = Bucket(counter + 1, dll_init())
            bucket_node = dll_append(self.bucket_head, bucket)
        elif next_bucket_node[2].counter != counter + 1:
            # bucket(counter + k) exist, insert bucket(counter + 1) BEFORE next_bucket_node
            bucket = Bucket(counter + 1, dll_init())
            bucket_node = dll_insert_before(next_bucket_node, bucket)
        else:
            # bucket(counter + 1) exists, use it
            bucket = next_bucket_node[2]
            bucket_node = next_bucket_node

        # Create the item, append it to the bucket and add to the cache.
        item = Item(key, value, bucket_node)
        self.cache[key] = dll_append(bucket.head, item)

    def set(self, key, value):
        # special case for capacity <= 0
        if self.capacity <= 0:
            return

        # Does the key exist in the cache?
        node = self.cache.get(key)
        if node:
            item = node[2]
            self.remove_node(node)
            self.add_node(item.key, value, item.bucket_node)
            return

        if len(self.cache) >= self.capacity:
            # Apply LRFU alogrithm here!
            bucket = self.bucket_head[1][2]
            self.remove_node(bucket.head[1])

        self.add_node(key, value, self.bucket_head)

    def get(self, key):
        node = self.cache.get(key)
        if node is None:
            return -1

        item = node[2]
        self.remove_node(node)
        self.add_node(item.key, item.value, item.bucket_node)
        return item.value

Check the memory leak

The memory leak is probably the biggest concern of a cache implementation, especially we are dealing with the circulated reference. Before declaring success, I’d like to run a benchmark to check the memory consumption first:

def setup():
    with open('lfu-cache-test-fixture.json') as f:
        fixture = json.load(f)
        cache = LFUCache2(2048)  # or LFUCache3
        return cache, fixture


def benchmark(cache, fixture):
    lut = {
        'set': cache.set,
        'get': cache.get
    }
    for method, args in zip(*fixture):
        lut[method](*args)
    gc.collect()

if __name__ == "__main__":
    print(timeit.timeit('benchmark(*setup())', setup='from __main__ import setup, benchmark', number=1000))

After installing memory_profiler, you may run the following command to sample memory consumption every 0.1s:

mprof run python lfu_benchmark.py
mprof plot

And the memory stats for both LFUCache2 and LFUCache3 look quite healthy.

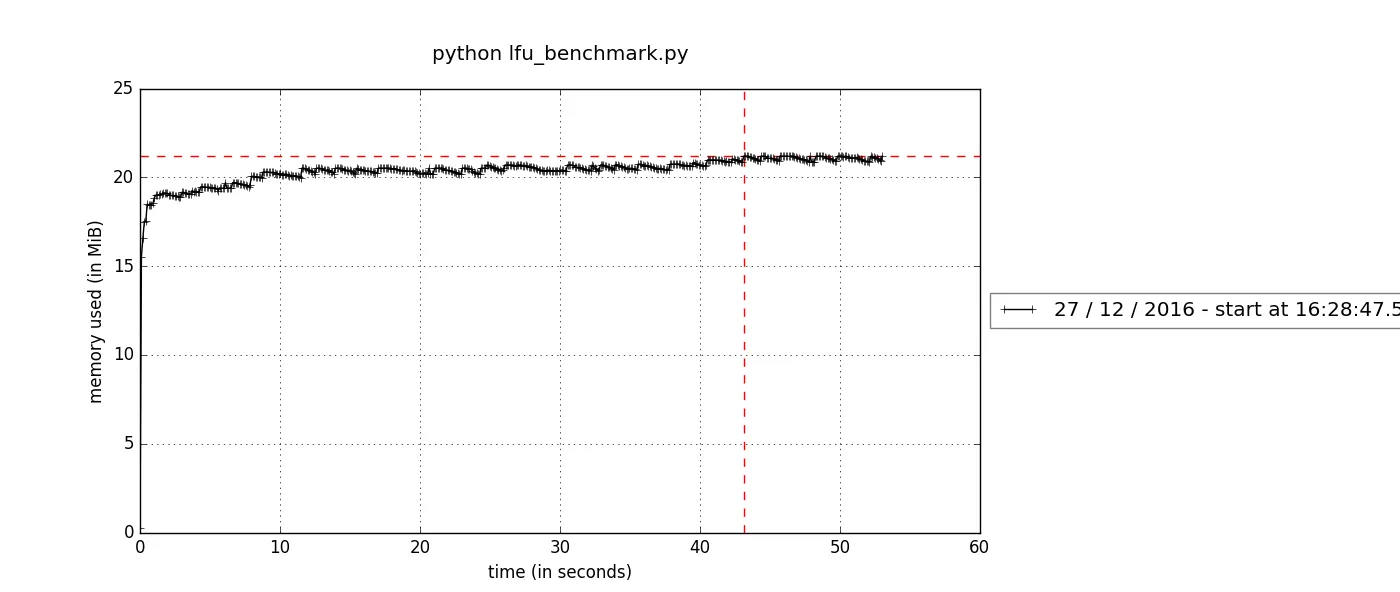
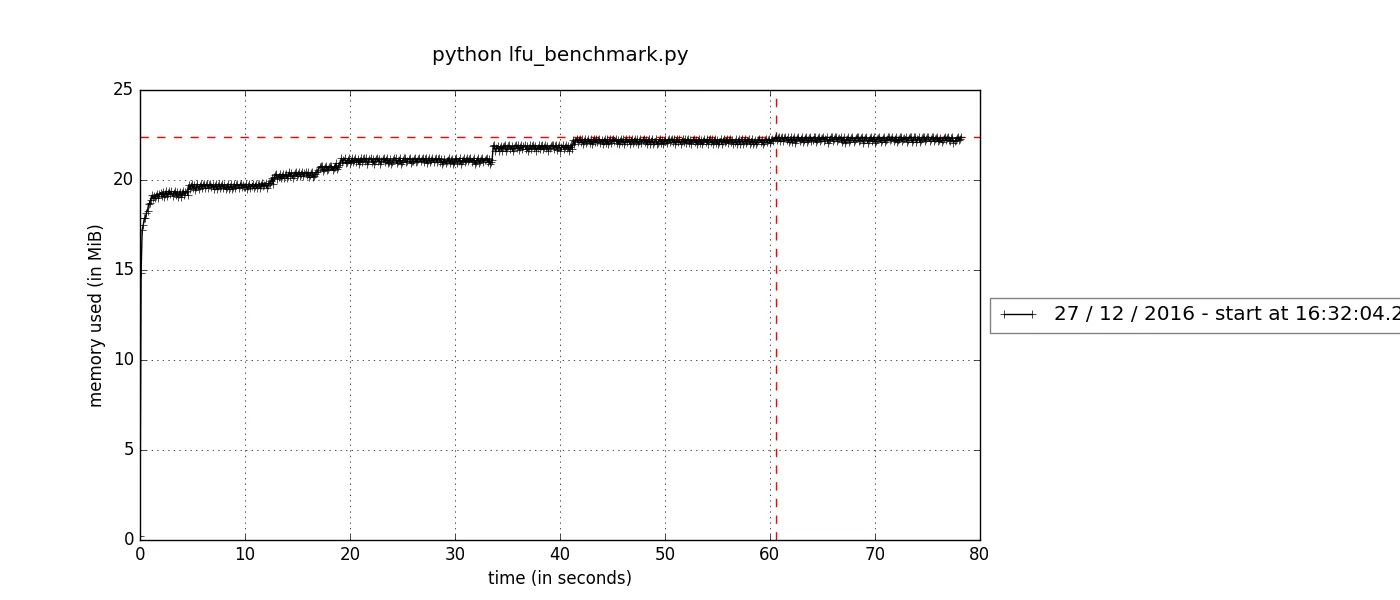
Please checkout my notebook if you prefer a backstage pass.

Technically, the combination of LFU algorithm and LRU algorithm is called LRFU. ↩

Track the accesses with doubly linked list

Put it in the bucket

Check the memory leak

Footnotes