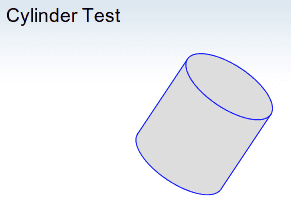
Moving forward: Cylinder
dojoCylinder is much more difficult to implement than the other polygon-based 3D objects. Polygon is still polygon after 3d projection, but the circle is mapped to ellipse and the we need to draw the the outline of surface by all means.
First thing first, we may reuse the cap later, so we introduce the
dojox.gfx3d.Orbit, which is the Circle in the 3D space, the first challenge is
how to map the X-Y plate circle to the 3D space orbit? We know the new center,
the semi major (this may not be true if the projection includes any scale of X,
Y, Z axis), and marks which are the projection of arbitrary points in the
original circle. The algorithm is inspired
bythis mathematic lecture.
- The general equation is: , we can normalize the marks according to the new center, the equation is reduced as:
- Let a = 1, the other parameters are determined by marks.
- The rotation angle, theta, is defined as .
- Then we can rotate the normalized mark by to get the canonical equation: .
- Using the marks again to find out and , which are the , and .
The draw procedure would create a Ellipse on with , rotate , then transpose to the center.
We could not use the Scene to simplify Cylinder drawing, since the curved surface is not a fixed rectangle. We draw the further cap first, then draw a rectangle with width of distance of two caps, height of major radius. A easier approach is to draw the path in (0, 0), rotate theta and transpose to the new center.
One picture is worthy the above. As usual, here is the snapshot.